che occorrerebbe per fare un brodo
con il lago di Ginevra."
"Ho finito di leggere Angels & Demons così ho capito tutto del CERN: il delitto deve essere sicuramente legato ad un furto di antimateria. Avete controllato i vostri... antidepositi... manca qualcosa?"
"Ispettore, per favore, non mi dirà che vuole condurre le indagini ispirandosi alla letteratura spazzatura!"
"Ma professore, ci sono un sacco di indizi in questa direzione. Probabilmente si tratta di una cellula di Al Qaeda che ha trafugato l'antimateria e adesso progetta di utilizzarla per un attacco terroristico. Ho notato che molti tecnici qui sono pakistani, chi ci dice che non siano infiltrati talebani che vengono a imparare le tecniche adatte a scatenare la nuova frontiera della jihad? Per esempio, cosa succederebbe se si inserisse dell'antiossigeno nei condotti dell'aria condizionata di una metropolitana di una grande città occidentale?"
"Credo che nella sua fantasiosa ricostruzione abbia tralasciato un particolare..."
"Sì, certo, la vittima! Probabilmente si è trovata al posto sbagliato al momento sbagliato durante il furto dell'antimateria e le è stata riservata questa fine atroce. Il tatuaggio sulla schiena potrebbe essere un tentativo di depistaggio, non mi stupirei se in occasione di un prossimo attentato si trovasse un libro di fisica delle particelle scritto in arabo in una macchina abbandonata!"
"No, ispettore, il particolare che ha tralasciato è che al CERN per ora siamo riusciti a produrre 9 atomi di antiidrogeno! E sa qual è l'energia che si può produrre con questi 9 atomi di antiidrogeno?"
"Abbastanza per distruggere Parigi, Londra e New York?"
"No, abbastanza per sollevare una zanzara di due micron."
"Accidenti. E che se ne fa Al Qaeda della zanzara sollevata di due micron?"
"Assolutamente nulla. Ecco perché la sua teoria non sta in piedi!"
"Ho capito" - rispose evidentemente contrariato l'ispettore - "comunque non è che mi porterebbe a vedere questi atomi di antiidrogeno?"
"Sono atomi, ispettore, non si vedono ad occhio nudo..."
"E come fate a sapere che ci sono?"
"Semplice, si mette l'antiidrogeno a contatto con l’idrogeno! Poi si vedono fotoni o pioni prodotti nell’annichilazione."
"E questi pioni sono più grandi?"
"Lasciamo stare, andiamo piuttosto a visitare il tracker!"
Fu allora che l'ispettore vide il Tracciatore.
Il cilindro, fissato alle estremità su un'impalcatura metallica, era formato da una serie di strati concentrici che, a mo' di buccia di cipolla, racchiudevano il punto dove sarebbe avvenuta la Prima Collisione.
Non poteva sapere – ma l'avrebbe dovuto avvertire nell'incanto di quella simmetria perfetta – che ognuno di quei piccoli rettangoli di silicio avrebbe contribuito a rilevare un segnale che, dopo il corretto allineamento dei raggi cosmici ottenuto grazie ad un algoritmo oscuro alle menti sublunari, avrebbe forse permesso di individuare la divina particella che necessariamente dona la massa a tutte le altre – facendo sì che la materia non si disperda nello spazio-tempo ma si riunisca a formare galassie, stelle, pianeti, montagne e oceani, piante e animali, i nostri stessi corpi, il segreto della fisica quantistica, la perfezione dell'universo.
Non è che l'ispettore pensasse in maniera così mistica e occulta per capriccio: aveva capito che solo cominciando a ragionare per associazioni, assonanze, sottotesti e implicazioni ultraterrene, avrebbe potuto risolvere il caso, perché quello era sicuramente il modo di procedere dell'assassino, che forse era un serial killer e avrebbe colpito ancora. Ma gli mancava la cultura necessaria, così la sua attenzione presto fu attratta da problemi più terra terra e, digiuno com'era di una sana formazione scientifica, azzardò una domanda pretenziosa.
"Mi dica, professore, come fate a progettare questo armamentario ed essere sicuri che, una volta che accenderete tutto, funzionerà come dovrebbe? Nel senso, per costruire una casa gli ingegneri sanno calcolare quanto deve essere spesso il muro portante, ma in questo caso..."
"Beh facciamo delle simulazioni..."
"Ah... e come fate a simulare tutte queste particelle che vanno in tutte le direzioni?"
"Fondamentalmente tiriamo dei numeri a caso!"
"Come dei numeri a caso? Per tornare all'esempio della casa... l'ingegnere non può mica tirare a caso lo spessore del muro se no..."
"...se gli ingegneri costruissero come i programmatori programmano, il primo picchio che passa distruggerebbe la civiltà... ma questa è un'altra storia. I nostri numeri sono tirati a caso ma poi ci ragioniamo sopra. Per esempio supponiamo che io voglia calcolare la superficie del lago di Ginevra."
"Eh, non è mica facile"
"Per nulla perché la forma non è regolare, non è che si può applicare qualche formulina semplice. Allora facciamo così... immaginiamo un rettangolo che racchiuda la superficie del lago..."
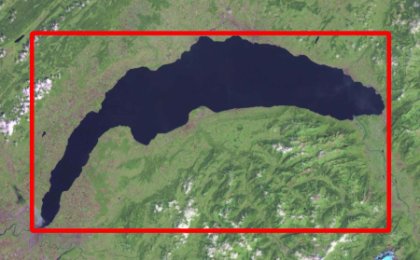
"a questo punto, supponendo di poterne misurare i lati, calcoliamo l'area del rettangolo"
"base per altezza, questa la so persino io, professore, però mi pare un metodo un po' grossolano"
"diciamo che questa è una stima per eccesso. Come facciamo per migliorarla? Iniziamo a tirare sassi nel lago."
"facendoli rimbalzare?"
"Non necessariamente. Per la precisione supponiamo di tirare i sassi secondo una distribuzione uniforme su tutta la superficie del rettangolo."
"Diamine, bisogna avere una bellla forza per arrivare nel mezzo"
"È un esperimento ideale, ispettore! Ma se gettiamo a caso nell'area del rettangolo cosa può succedere?"
"Che magari non facciamo centro e becchiamo uno spettatore del festival jazz di Montreux."
"Esatto, allora facciamo così: dopo aver gettato il sasso aspettiamo di sentire SPLASH... Contiamo il numero totale di sassi ed il numero di splash. Poi stimiamo l'area del lago così: dividiamo l'area del retangolo per il numero totale di sassi e moltiplichiamo per il numero di splash."
"Ma quanti sassi ci vogliono?"
"Parecchi, ma per fortuna abbiamo i computer che lanciano i sassi per noi in dei laghi a n dimensioni! perché, vede, finché il lago è in due dimensioni si potrebbe anche tentare di calcolare la superficie in un altro modo, ma quando il numero di dimensioni è grande... bisogna tirare i sassi. Si chiamano metodi di Monte Carlo, per via del famoso casinò."
(3 - continua...)
2 commenti:
ASSOLUTAMENTE GENIALE!! Maso sei il mio Dan Brown di fiducia.
Stai targiversando troppo: puo' essere il "sonno arretrato"...oppure era la casa di Cointrin che ti dava l'ispirazione?
Posta un commento